Fort Marinus

As I sit in my 30th storey flat, looking over a SimCity-esque grid of city buildings and rooftops, I wonder, “How far away is the horizon?” At what distance do those concrete and brick structures fade into obscurity? If I squint hard, can I see Russia?

First, let us assume perfect visibility and ignore light-bending particle interference et cetera. In general, surprisingly, the distance to the horizon [D] depends on only two factors: 1) the radius of the Earth [R] and 2) the observer’s height from the ground [H].

In short,           ,           

The radius of the Earth (R) is about 3963 miles. The 30th floor [H] is about 0.056 miles high (assume 10 feet per floor times 30 floors, all divided by 5280 feet per mile). Plugging that information into our equation, , we find that the horizon is about 21 miles away.

Now, suppose I am standing on the beach looking out toward the horizon. How far can I see? The radius of the earth has not changed. But now I am only .001 miles off the ground (somewhere between 5 and 6 feet). Our equation becomes The horizon is about 2.8 miles away. That’s it!

Trigonometry ahead

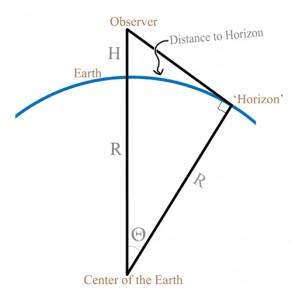Where does that lovely equation come from? Draw a diagram. Draw the Earth as a perfect two-dimensional circle. Also draw two radius lines; one terminating at the observer’s location, the other at the horizon. The lines form a triangle. Geometrically, the ‘horizon’ is the point at which one’s line-of-sight becomes tangent with the circle. By definition, the fact that the line-of-site is tangent to the circle means that the angle there is 90 degrees; the so-called ‘Right Triangle’.

Since we have a Right Triangle, we can use the Cosine trigonometric function to describe the angle that is the ‘slice’ of Earth between the Observer and the Horizon, call it Θ. In Right Triangles, the Cosine of an angle is described as the side Adjacent to it divided by the Hypotenuse. In our case, . We can solve for Θ by taking the Inverse Cosine of both sides of the equation, leaving: .

Now, the Distance to the Horizon is an ‘arc length’: mathematically defined as the radius times the angle of the ‘slice’, R · Θ. We previously solved for Θ, so we can plug it in, yielding the final equation of Distance-to-Horizon = .