Fort Marinus

For Christmas, I received John Evans’ “Adventures with Pinhole and Homemade Cameras” book. It is actually a book and kit with materials to build your own Pinhole camera. The final product is a cardboard film camera whose lens is a brass plate with a .15mm laser-cut hole. Ultimately, I didn’t built the camera. Instead, I harvested the brass plate and mounted it to a spare body cap for use on my digital camera. Here’s what I came up with.

Instead of a glass lens, a Pinhole Camera uses a very small hole to let in shafts of light. Since the hole is so small, exposure times need to be longer than a typical photograph. The resulting images are often soft, blurry, and abstract, but not always. This is my first time playing around with one, we’ll see what I can do with it. MORE PICTURES TO COME!

The daytime pinhole picture looks like a low quality photograph. The nighttime picture of a bookcase looks more like I snapped a photo of a ghost.

“[C]hurches are not simply gathering places but signify and make visible the Church living in its place, the dwelling of God […]” – CCC 1180.ⁱ

St. Joseph’s Byzantine Rite Catholic Church was completed in 1933 to serve part of Cleveland’s Carpatho-Rusyn population. The Rusyns are an Eastern Slavic ethnic group originally inhabiting the Carpathian Mountain region; primarily near the borders of modern day Hungary, Ukraine, Slovakia, and a small part of Poland.ⁱⁱ

As the story goes, in the 9^th century, Saints Cyril and Methodius brought Christianity to the Slavic peoples.ⁱⁱⁱ Most of the Rusyns, sometimes called Ruthenians, practiced Orthodox Christianity until the 17^th century when they became part of the Catholic Church. In the late 1800s, many Rusyns came to Cleveland, establishing several Byzantine Catholic churches in the area.^iv

St. Joseph’s is the second building to occupy the site, replacing a smaller structure first built in 1913.^v The current building was designed by Polish-American architect Joseph E. Fronczak.[^vi and.^vii] By the late 1970s, the congregation relocated to Brecksville, Ohio. They sold the church building to the Zion Baptist Church who used it for a time but ultimately abandoned the structure. As of 2011, the building is in a state of disrepair despite being a one of Cleveland’s 305 Designated Landmarks.^viii

The brick-façade church is a simple Romanesque-style building; characterized by rounded archways, symmetrical bell towers, a central nave, and two flanking side aisles supported by columns with Corinthian-inspired capitals. Open and empty, the windows no doubt once held stained glass.

Wind and rain have eroded the interior, revealing the underlying metal structure. It seems that some persons have thoroughly torn up the floor; though, curiously, they left the floor boards heaped in place. Surprisingly, the place is free from graffiti. The space is empty of any furniture or fixtures. The main altar and baldacchino, four side altars, and all of the pews are missing, perhaps relocated? Only some architectural ornamentation and fading murals remain.

The largest and most preserved mural is above the altar, in the apse. The Christ-child is in the center, radiating divine light. He is joined on either side by his Earthly parents, Mary and Joseph, for whom the church is named. Directly above is God the Holy Spirit as a dove and God the Father as an aged man with triangular halo. Flanking on the left is Moses holding the Ten Commandments and on the right is John the Baptist. Incense-bearing angels and winged cherubs attend the holy figures in a celestial cloudscape.

Various biblical and ecclesiastical scenes decorate the barrel vaulting; most are damaged by water, causing the paint to fade and the plaster to crumble. See^ix and^x and^xi and^xii and^xiii .

St. Joseph’s time as a living structure was architecturally brief, only 40 or so years. It has been vacant for nearly as long.  The building seems to be structurally sound; the support beams are intact and the exterior shows only minor cracking. Perhaps it could be re-used once again. Though, given the economic situation of the area, it seems likely that old St. Joseph’s will continue to decay beyond repair. Alas, although cheerless to see a fine piece of architecture go to waste, more precious treasures have become Forgotten Places of the World.

1. http://books.google.com/books?id=rEGcXz8GT3sC&pg=PA305&lpg=PA305&dq=catechism+of+the+catholic+church+no+1180&source=bl&ots=LX9OY3W21x&sig=jorUlGc8iOjUWXpqhKsU43WN8B8&hl=en&ei=w6OjToeeGcrAgQfQx7jEBQ&sa=X&oi=book_result&ct=result&resnum=5&ved=0CEMQ6AEwBA#v=onepage&q&f=false [↩]
2. http://en.wikipedia.org/wiki/Rusyns [↩]
3. http://en.wikipedia.org/wiki/Cyril_and_Methodius [↩]
4. http://ech.cwru.edu/ech-cgi/article.pl?id=R8 [↩]
5. http://www.stjoebyz.com/?history [↩]
6. http://communities.aia.org/sites/hdoaa/wiki/AIA%20scans/Rosters/FronczakJosephE_roster.pdf [↩]
7. http://ampoleagle.com/joseph-e-fronczak-br-the-villa-maria-college-architect-p4834-112.htm [↩]
8. http://planning.city.cleveland.oh.us/landmark/landlist_alpha.php?first=G [↩]
9. http://www.biblegateway.com/passage/?search=Luke%202:8-21&version=DRA [↩]
10. http://www.biblegateway.com/passage/?search=Luke%201:26-38&version=DRA [↩]
11. http://www.biblegateway.com/passage/?search=Genesis%2022:1-19&version=DRA [↩]
12. http://www.biblegateway.com/passage/?search=Genesis%2014:18&version=DRA [↩]
13. http://www.biblegateway.com/passage/?search=Acts%2022:20&version=DRA [↩]

“You can change the rules, but you can’t change history.” – Nike Running.

Fort Marinus’ logo forms part of Nike’s “Own Chicago” Mosaic.

It makes up several small tiles in the blue-ish area above the ‘W’. Can you spot them?

http://www.facebook.com/nikerunning?sk=app_106056822837554

“Because it’s there.” – G. H. Mallory, when asked why he wanted to climb Mount Everest.

Michigan Central Station, built in 1913 for the Michigan Central Railroad, was Detroit’s passenger rail depot from its opening until Amtrak discontinued service in 1988. Architecturally, the building is Beaux-Arts, designed by Warren & Wetmore and Reed & Stem, who also designed New York City’s Grand Central Terminal. The 500,000 square-foot building cost $15 million when built (about $328 million in 2011 currency). It featured beautiful stonework, terra cotta ornamentation, wide vaulted ceilings, and decorated interiors. (source)

Now abandoned, and (mostly) empty, this impressive structure just sits there, boarded up, rotting away in its own filth. It is actually quite beautiful. Most passers-by overlook the landmark; it even passes for a living building when viewed from afar. Once the main transportation hub of the bustling Motor-City, the Station is now one of the Forgotten Places of the World.

Forgotten by most, but not by all – A brave few Urban Explorers have gone deep inside to bring back photo reconnaissance. They are part-time archaeologists of the Indiana Jones variety. Sometimes foolish, always unlicensed; the Urban Explorer hunts the forgotten places of the world and returns with a story to tell.

The side entrance is a large open doorway, black and unknown; broken glass and graffiti for a welcome mat. Only the frames and a few tattered shards of glass remain of the windows, leaving the interior exposed to the elements. Who lurks in the darkness? What prowls in the deep? The question is not really if someone or something has been inside; the question is, “are they in there right now?”.

Once inside, the view becomes wide and high with the sight of the Main Waiting Room. Somehow the room is grand even in its dilapidated state. Chunks of plaster have fallen, revealing the underlying brick structure. Marble and terra cotta ornamentation lie shattered on the ground. The terrazzo designwork is barely visible on the faded and unpolished floors. Vandals have made a canvas of the walls.

Continuing on the first floor, the Main Room adjoins the Concourse, an equally large sky-lit room leading out to the platforms. Nearby, the ticket counters, baggage area, and even a grand dining room remain. In the dining room, a lattice of thin metal bars traverses the groin vaulting; perhaps leftover from a late-addition drop ceiling. Gasp!

The upper levels are more utilitarian than the first. Floor after floor of symmetrical corridors are painted eggshell with fading pastel accents. The hallways are surprisingly well lit because of the old fashioned ventilation windows above the doors. Most rooms are empty, furnished only by the original floorboards that have buckled from exposure. Occasionally, a graveyard of vinyl floor tiling litters the ground; no doubt the product of some hasty mid-century renovation. Each floor plan is identical, save for the top double-level floor which is mysteriously empty.

At last, the photographers arrive on the roof just in time to catch a glowing sunset. The future of this building is unclear. It has managed to avoid demolition over the last 23 years. But those 23 years have been wearisome, leaving a shell of a building that seems too far gone for a cost effective renovation. Perhaps it will remain there, aging until it becomes but an ancient ruin.

As I sit in my 30th storey flat, looking over a SimCity-esque grid of city buildings and rooftops, I wonder, “How far away is the horizon?” At what distance do those concrete and brick structures fade into obscurity? If I squint hard, can I see Russia?

First, let us assume perfect visibility and ignore light-bending particle interference et cetera. In general, surprisingly, the distance to the horizon [D] depends on only two factors: 1) the radius of the Earth [R] and 2) the observer’s height from the ground [H].

In short,           ,           

The radius of the Earth (R) is about 3963 miles. The 30th floor [H] is about 0.056 miles high (assume 10 feet per floor times 30 floors, all divided by 5280 feet per mile). Plugging that information into our equation, , we find that the horizon is about 21 miles away.

Now, suppose I am standing on the beach looking out toward the horizon. How far can I see? The radius of the earth has not changed. But now I am only .001 miles off the ground (somewhere between 5 and 6 feet). Our equation becomes The horizon is about 2.8 miles away. That’s it!

Trigonometry ahead

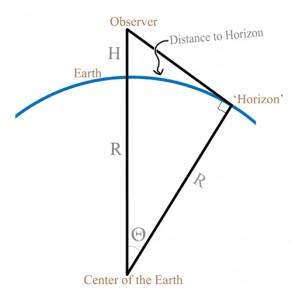Where does that lovely equation come from? Draw a diagram. Draw the Earth as a perfect two-dimensional circle. Also draw two radius lines; one terminating at the observer’s location, the other at the horizon. The lines form a triangle. Geometrically, the ‘horizon’ is the point at which one’s line-of-sight becomes tangent with the circle. By definition, the fact that the line-of-site is tangent to the circle means that the angle there is 90 degrees; the so-called ‘Right Triangle’.

Since we have a Right Triangle, we can use the Cosine trigonometric function to describe the angle that is the ‘slice’ of Earth between the Observer and the Horizon, call it Θ. In Right Triangles, the Cosine of an angle is described as the side Adjacent to it divided by the Hypotenuse. In our case, . We can solve for Θ by taking the Inverse Cosine of both sides of the equation, leaving: .

Now, the Distance to the Horizon is an ‘arc length’: mathematically defined as the radius times the angle of the ‘slice’, R · Θ. We previously solved for Θ, so we can plug it in, yielding the final equation of Distance-to-Horizon = .

“I’ve dranken a lot more than I drank tonight.” – Ron of the Jersey Shore.

I happened upon this sound bite as I cycled through the channels, lamenting the fact that ‘there’s nothing good to watch on TV’. No, seriously, I was only flipping channels; I don’t really watch this show. It’s true! No need to pick on Ron though. I have heard various mutations of drank, drunk, ‘dranken’, and drunken in common speech. Perhaps it is a bit confusing. Many tend to avoid the construction completely. Fear not, be confident as you conjugate ‘drank’, and allow me to take you to school:

TENSE                     EXAMPLE
Present                   "He drinks"
Past                      "He drank"
Future                    "He will drink"
Present  Perfect          "He has drunk"
Past     Perfect          "He had drunk"
Future   Perfect          "He will have drunk"
Present  Conditional      "He would drink (if...)"
Perfect  Conditional      "He would have drunk (if...)"

Returning to Ron, we imagine that he meant to convey that he had done more drinking in the past than the drinking that occurred that evening. Speaking from the present time, he first references past completed events: this is called the ‘Perfect’ tense. He might say, “I have drunk”. Next, he speaks of a past event without reference to its completedness: this is called the ‘Simple Past’ tense. He might say, “than I drank tonight”. Assembling the phrase, we have “I have drunk a lot more than I drank tonight”.

The phrase sounds a bit archaic perhaps. The modern ear may even prefer ‘dranken’, as it matches the paradigm for ‘eaten’ or ‘written’ for example. Ironically, ‘dranken’, though not proper English of any kind, sounds like the Old English Past Participle word form, ‘druncan’.

But, language is a funny thing. If we clearly understand the meaning of something, when does correction become pedantic?

For my first post, I would like to share this luxurious swatch of fabric. This is Herringbone.

Herringbone describes a wonderful pattern of woven fabric, so called (supposedly) because it ‘resembles the bone structure of a herring fish’. Typically uninteresting when used for woolen outerwear, as is most common, Herringbone is decidedly luxurious when used with high thread count cotton as in a fine dress shirt. In this case, it exudes a subtle yet radiant sheen that evokes an air of sophistication and style. The effect is inarticulable by most, but noticed by all.